leetcode经典例题第三题,关于求坐标共线问题。
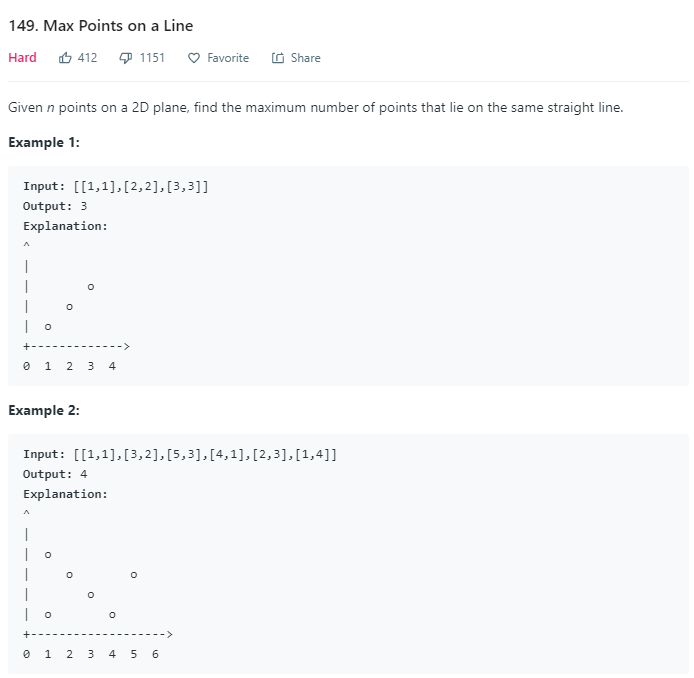
题目描述
解题思路
点共线,那么最容易想到的思路就是确定斜率,斜率相同不就共线了。但是还有两点特殊情况需要考虑,二是当两个点重合时,无法确定一条直线,但这也是共线的情况,需要特殊处理。二是斜率不存在的情况,由于两个点(x1, y1)和(x2, y2)的斜率k表示为(y2 - y1) / (x2 - x1),那么当x1 = x2时斜率不存在,这种共线情况需要特殊处理。这里我对重合的情况,斜率不存在的情况以及斜率为0的情况进行了讨论,因为这比较好处理,所以处理一下斜率为0的没什么问题。最后就是通用情况,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public int maxPoints(Point[] points) {
if(points == null){
return 0;
}
if(points.length <= 2){
return points.length;
}
Map<Double,Integer> map = new HashMap<>();
int result = 0;
for(int i=0;i<points.length;i++){
map.clear();
int overlap = 0;
int vertical = 0;
int horizon = 0;
int max = 0;
double rate = 0.0;
for(int j=i+1;j<points.length;j++){
double gapx = new Double(points[i].x) - new Double(points[j].x);
double gapy = new Double(points[i].y) - new Double(points[j].y);
if(gapx == 0 && gapy == 0){
overlap++;
continue;
}else if(gapx == 0){
vertical++;
max = Math.max(max,vertical);
}else if(gapy == 0){
horizon++;
max = Math.max(max,horizon);
}else{
rate = gapy/gapx;
if(map.containsKey(rate)){
map.put(rate,map.get(rate)+1);
}else{
map.put(rate,1);
}
max = Math.max(max,map.get(rate));
}
}
result=Math.max(result, max+overlap+1);
}
return result;
}
}
|
虽然可以在牛客上通过,但是这个思路在leetcode上已经不行了,它给的例子是:
1
2
3
| Input [[0,0],[94911151,94911150],[94911152,94911151]]
Output 3
Expected 2
|
我们注意到,由于精度丢失问题,我们算出来的斜率竟然是一样的了,所以这个程序错误地认为这三个点都共线了。因此错误。那怎么办呢?
代码提交
由于通过斜率来判断共线需要用到除法,而用double表示的双精度小数在有的系统里不一定准确,为了更加精确无误的计算共线,我们应当避免除法,从而避免无线不循环小数的出现,那么怎么办呢,我们把除数和被除数都保存下来,不做除法,但是我们要让这两数分别除以它们的最大公约数,这样例如8和4,4和2,2和1,这三组商相同的数就都会存到一个映射里面,同样也能实现我们的目标。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class Solution {
public int maxPoints(Point[] points) {
if(points == null){
return 0;
}
if(points.length <= 2){
return points.length;
}
Map<Map<Integer,Integer>,Integer> map = new HashMap<>();
int result = 0;
for(int i=0;i<points.length;i++){
map.clear();
int dup = 1;
int max = 0;
for(int j=i+1;j<points.length;j++){
int x = points[i].x - points[j].x;
int y = points[i].y - points[j].y;
if(x == 0 && y == 0){
dup++;
continue;
}
int d = gcd(x, y);
Map<Integer,Integer> tmpMap = new HashMap<>();
tmpMap.put(x/d,y/d);
map.put(tmpMap, map.getOrDefault(tmpMap, 0) + 1);
max = Math.max(max,map.get(tmpMap));
}
result = Math.max(result,max+dup);
}
return result;
}
public int gcd(int a, int b) {
return (b == 0) ? a : gcd(b, a % b);
}
}
|
